티스토리 뷰
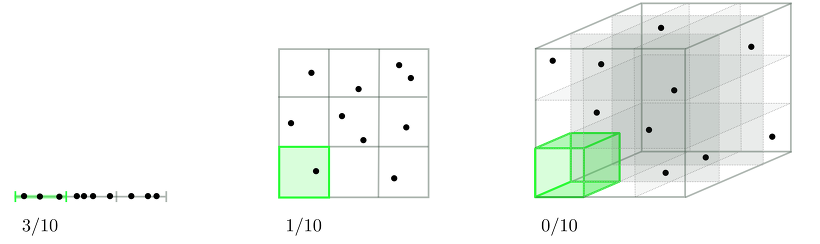
머신러닝 모델의 성능을 저하시키는 한 요인은 데이터의 Feature 수가 많아 학습 속도가 느리고 성능이 낮아지는 '차원의 저주' 현상 때문입니다. 차원이 증가할수록 설명력을 유지하기 위한 데이터의 양이 증가하는 것과 아래 그림처럼 차원이 증가할수록 데이터 포인트 간의 거리는 증가하고 의미 없는 공간이 커져 성능이 저하되는 것입니다.
차원의 저주를 해결할 수 있는 기법 중 하나인 PCA, 주성분 분석은 데이터 내 존재하는 노이즈(Noise)을 제거하고 축소된 차원 덕에 연산량이 줄어드는 효과를 가집니다. 즉, PCA의 가장 중요한 원리는 데이터의 차원을 어떻게 축소시키는 것입니다.
수학적으로 차원을 축소하는 것을 '투영(Projection)'이라고 합니다. 투영은 N차원 공간의 데이터를 (N-1)차원 공간의 데이터로 만드는 것입니다. 이와 같이 PCA는 투영을 통해 차원을 축소하고 투영을 위한 기준이 필요합니다. 그 기준은 데이터의 분산이 최대가 되는 축입니다.
PCA가 이루어지는 단계는 다음과 같습니다.
- 데이터셋에서 분산이 최대가 되는 축을 찾는다.
- 찾은 첫번째 축과 직교하면서 분산이 최대가 되는 축을 찾는다.
- 첫 번째 축과 두 번째 축에 직교하고 분산이 최대가 되는 축을 찾는다.
- 1 ~ 3과 같은 방법으로 데이터 셋의 차원만큼 축을 찾는다.
이러한 PCA는 공분산 행렬의 영향을 받습니다. '공분산'은 2개 변수 간의 상관 정도와 데이터가 분포하는 정도를 알 수 있는 지표입니다. 데이터의 분산을 최대로 보존하는 축을 찾기 위해서는 공분산을 활용해 PCA을 구할 수 있습니다

n개의 Feature와 m개의 관측치를 가진 데이터의 공분산은 다음과 같습니다. 이를 통해, 데이터의 분산이 최대가 되는 축을 찾아 데이터셋을 임의의 단위벡터로 새로운 축에 투영시킬 수 있습니다.
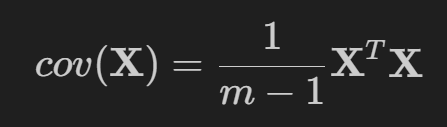

만약, 데이터가 크기가 n인 정방행렬의 형태라면 선형대수학의 '고유값 분해'를 통해 고윳값과 고유벡터를 찾아 PCA을 찾을 수 있습니다. 고윳값은 고유벡터가 변화되는 조정값을 의미하고, 고유벡터는 선형결합에도 보존되는 방향을 의미합니다.
정방행렬 A가 있을 때 Ax = λx을 만족하는 λ 을 찾는 '고유값 분해'를 활용한 PCA는 λ을 통해 데이터의 숨은 특성을 상수배를 통해 찾는 원리입니다. 하지만 우리의 데이터는 정방행렬의 형태를 가지지 않는 경우가 매우 많습니다. 정방행렬이 아닌 m X n 형태에서는 '특이값 분해'를 통해 PCA을 구할 수 있습니다

특이값 분해는 A^TA 행렬의 고윳값을 루트 취하여 특이값을 구하고, 그에 따른 고유 벡터를 찾아 분해하는 것입니다. V가 A^TA 행렬의 정규직교하는 고유벡터의 열행렬일 때, U는 {AV1, Av2, ----, AVn}을 정규화한 벡터의 열행렬입니다. 즉, U을 구하기 위해서는 각 위치에 맞는 고윳값과 U 집합의 원소를 곱해서 구할 수 있습니다.
이와 같은 특이값 분해는 고유값 분해가 정방행렬에서만 활용할 수 있다는 한계를 해결하고, PCA을 구할 수 있는 라이브러리인 sklearn에서는 특이값 분해가 공분산 행렬을 따로 메모리에 저장할 필요가 없이 구현되어 더욱 연산량 적으로 효율적이다.
'머신러닝' 카테고리의 다른 글
| [8] 의사결정나무 (2) | 2024.06.30 |
|---|---|
| [7] 앙상블 모델 (0) | 2024.06.28 |
| [5] KMeans 알고리즘 (0) | 2024.05.15 |
| [4] Support Vector Machine(SVM) (0) | 2024.05.12 |
| [3] K 근접 이웃 알고리즘(knn) (0) | 2024.05.10 |
- randomforest #bagging #머신러닝 #하이퍼파라미터 튜닝
- 자연어 처리 #정제 #정규표현식 #어간 추출 #표제어 추출
- #물고기 종류별 대어 찾기 #즐겨찾기가 가장 많은 식당 정보 출력하기 #mysql #programmers
- #tf idf
- #자연어 처리 #정수 인코딩 #빈도 수 기반
- 로지스틱 회귀 #오즈비 #최대우도추정법 #머신러닝
- #opencv #이미지 읽기 #이미지 제작 #관심영역 지정 #스레시홀딩
- # 할인행사 #counter #딕셔너리 #프로그래머스
- 머신러닝 #xgboost #
- 머신러닝 #lightgbm #goss #ebf
- nlp #토큰화 #nltk #konply
- #django #mvt 패턴
- #python #프로그래머스 #외계어사전 #itertools #순열과조합
- 머신러닝 #project #classification #dacon
- #프로그래머스 #안전지대 #시뮬레이션
- # 프로그래머스 #연속된 부분수열의 합 #이중 포인터 #누적합
- #with recursive #입양시각 구하기(2) #mysql
- 프로젝트 #머신러닝 #regression #eda #preprocessing #modeling
- #웹 프로그래밍 #서버 #클라이언트 #http #was
- # 프로그래머스 # 카펫 # 완전탐색
- pca #주성분분석 #특이값분해 #고유값분해 #공분산행렬 #차원의 저주
- #attention #deeplearning
- #opencv #이미지 연산 #합성
- #docker #docker compose
- #docker #container #docker command
- python #프로그래머스 #겹치는선분의길이
- #polars #대용량 데이터셋 처리
- 잘라서 배열로 저장하기 #2차원으로 만들기
- #docker #image #build #dockerfile
- #seq2seq #encoder #decoder #teacher forcing
