티스토리 뷰
머신러닝 카테고리의 네 번째 글에서는 지도학습 중 하나로 새로운 data를 미리 정의된 label 중 하나로 분류하는 K 근접 이웃 알고리즘(K nearest neighbor algorithm)에 대한 설명과 동작원리에 대해 설명하겠습니다.
K 근접 이웃 알고리즘(knn)은 거리 기반으로 새로운 data를 미리 정의된 label 중 하나로 분류하는 알고리즘입니다.
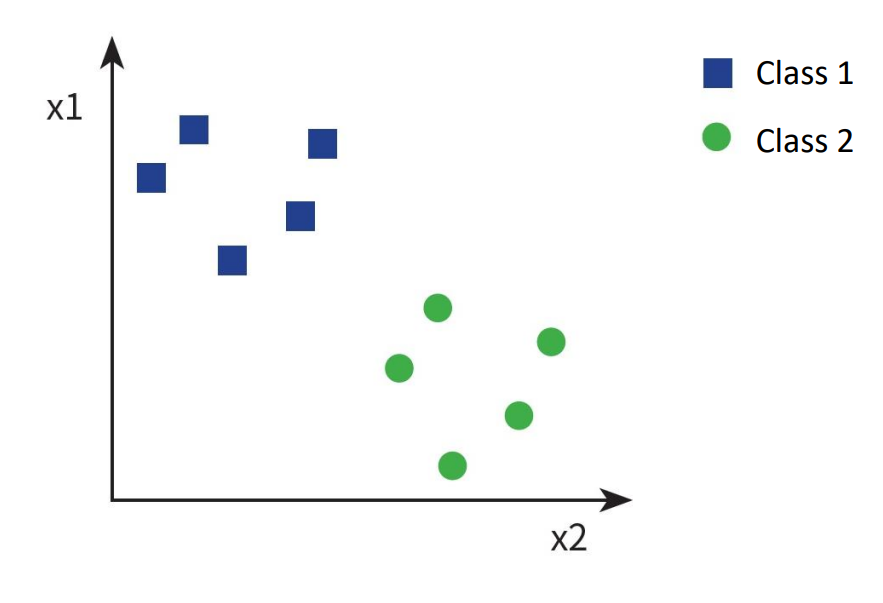
knn은 위 그림처럼 label이 정해진 데이터에 한해서 분류를 진행하는 지도학습 알고리즘의 종류입니다. 데이터가 적은 상황에서도 간단한 모델로 높은 분류 정확도를 가지는 것이 가장 큰 장점입니다.

knn 알고리즘의 동작 원리는 학습 데이터와 새로운 데이터 간의 거리를 측정하여 가장 가까운 k개의 data들의 label 중 가장 많은 비율을 차지하는 label로 새로운 데이터를 분류하는 것입니다. 위 그림을 예시로 동작원리를 설명하자면, 새로운 data(빨간색 별)과 가장 가까운 거리의 data의 개수를 3개(class1 1개, class2 2개)로 설정하면, 가장 많은 비율을 차지하는 class2로 새로운 data의 class를 분류할 수 있습니다. 반면 가장 가까운 거리의 data의 개수를 5개로 설정하면 새로운 data는 class1으로 분류할 수 있습니다.
이처럼 knn 알고리즘은 학습 데이터를 설정하고 새로운 데이터와 학습 데이터 간의 거리를 측정하는 것부터 시작합니다. 이때 거리를 측정하는 방법은 매우 다양합니다.
- 유클리디안 거리(L2 distance)
- 맨해튼 거리(L1 distance)

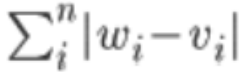
위와 같은 방식으로 거리를 측정한 후 거리가 작은 k개의 data 중 label의 비율이 가장 많은 것으로 새로운 데이터의 label을 결정합니다. knn 알고리즘의 성능을 결정하는 것은 k값을 얼마로 설정하는 것입니다. k값을 임의로 설정할 수 있지만 데이터의 특성을 반영하여 가장 성능이 좋은 k값을 설정할 수 있는 방법이 존재합니다. 바로 교차검증입니다.
교차 검증(Cross Validation)은 방법은 전체 데이터셋을 train 데이터와 validation 데이터로 분리한 후 반복적으로 학습을 돌린 후 평균 성능이 가장 높은 k개를 설정하는 방법입니다.

교차 검증을 이용하여 knn 알고리즘의 k값을 설정하면 과적합을 해결할 수 있습니다. 만약 전체 데이터셋을 모두 train data로 사용하면 학습 정확도만 높아지는 현상이 발생합니다. 따라서 구현한 모델의 타당한지를 보여주는 validataion 데이터셋과 예측에 사용하는 test 데이터셋을 전체 데이터셋에서 설정하여 학습을 반복한 후 각각의 성능이 가장 좋은 k값으로 설정하는 것이 교차 검증의 원리입니다.
교차 검증에서 더 나아가 k fold 교차 검증이라는 방법이 존재합니다. k fold 교차 검증은 k개의 fold를 설정해서 학습을 진행하는 것입니다.

위 그림 같은 경우는 k값을 5로 설정해 5개의 fold를 설정한 예입니다. 그림에서와 같이 validation data를 1개의 fold로 설정하고 나머지 fold는 모두 train data로 설정합니다. 하나의 데이터셋에 대한 학습이 끝나면 랜덤 하게 validation data에 해당하는 fold를 바꿔가면서 지정해 모델을 생성하고 에러값을 산출하는 과정을 반복합니다. 결과적으로는 에러값이 가장 적은 모델을 찾고 해당하는 k값을 결정하는 것입니다.
knn 알고리즘의 k값을 이와 같은 과정을 통해 구하면 다양한 문제점을 해결할 수 있습니다. 만약 k값을 임의로 설정할 때, 크게 작으면 데이터의 세부적인 특성을 섬세하게 파악하기 어려운 문제점이 있습니다. 반면 k값을 작게 설정하면 데이터의 이상치를 포함하기 쉬워 성능을 떨어뜨리는 문제점이 발생합니다.
knn 알고리즘은 머신러닝 중 분류 알고리즘에 해당하는 가장 성능 높은 알고리즘입니다. 분류 알고리즘은 품질 분석에서 불량품을 분류하거나 특정 품종을 분류하는 등 다양한 분야에 활용될 수 있습니다.
[Reference]
홍익대학교 컴퓨터공학과 기계학습심화 수업 ppt
'머신러닝' 카테고리의 다른 글
| [5] KMeans 알고리즘 (0) | 2024.05.15 |
|---|---|
| [4] Support Vector Machine(SVM) (0) | 2024.05.12 |
| [2] 선형회귀 (0) | 2024.05.05 |
| [1] 머신러닝의 분류와 과적합 (0) | 2024.05.03 |
| [0] 머신러닝이란? (1) | 2024.05.01 |
- #with recursive #입양시각 구하기(2) #mysql
- #물고기 종류별 대어 찾기 #즐겨찾기가 가장 많은 식당 정보 출력하기 #mysql #programmers
- pca #주성분분석 #특이값분해 #고유값분해 #공분산행렬 #차원의 저주
- 머신러닝 #project #classification #dacon
- #opencv #이미지 연산 #합성
- #python #프로그래머스 #외계어사전 #itertools #순열과조합
- #docker #docker compose
- #django #mvt 패턴
- #docker #image #build #dockerfile
- #attention #deeplearning
- #opencv #이미지 읽기 #이미지 제작 #관심영역 지정 #스레시홀딩
- 잘라서 배열로 저장하기 #2차원으로 만들기
- 로지스틱 회귀 #오즈비 #최대우도추정법 #머신러닝
- 머신러닝 #xgboost #
- nlp #토큰화 #nltk #konply
- randomforest #bagging #머신러닝 #하이퍼파라미터 튜닝
- #tf idf
- #자연어 처리 #정수 인코딩 #빈도 수 기반
- 머신러닝 #lightgbm #goss #ebf
- #polars #대용량 데이터셋 처리
- # 프로그래머스 #연속된 부분수열의 합 #이중 포인터 #누적합
- # 프로그래머스 # 카펫 # 완전탐색
- 자연어 처리 #정제 #정규표현식 #어간 추출 #표제어 추출
- # 할인행사 #counter #딕셔너리 #프로그래머스
- #웹 프로그래밍 #서버 #클라이언트 #http #was
- #프로그래머스 #안전지대 #시뮬레이션
- 프로젝트 #머신러닝 #regression #eda #preprocessing #modeling
- #seq2seq #encoder #decoder #teacher forcing
- #docker #container #docker command
- python #프로그래머스 #겹치는선분의길이
